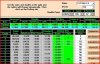
I have an idea for disguising advantage play based largely on bluewhale's earlier post...
As I understand it, raising bets as the count goes up and lowering bets when the counts go down is a dead-giveaway for a CC/AP. If a TC of one or greater means a net advantage over the house, why not incorporate a random multiplier/divisor into the bet?
Normally, when it comes time to bet, you determine your RC, calculate your TC, subtract 1 and that gives you the bet unit multiplier. If your bet unit is $10 and your multiplier is 3, you'd be $30, etc, etc.
Just for visualization purpose, suppose you had a 7-sided with you but instead of 1-7 on the dice, you'd have -3 through +3 (-3, -2, -1, 0, 1, 2, 3). At any multiplier >=1, you'd roll the dice and adjust your bet accordingly.
This means that sometimes you'd start with unit multiplier of 4, roll the dice, get -2 and wind up placing a $20 bet. Other times you'd start with a unit multiplier of 2 and roll +3 and be betting $50.
How does this effect the game in total?
1) Your betting appears chaotic during the short-term (ie, the time during which you're being observed for AP). Sometimes you're at an advantage and betting flat, sometimes you're at barely a positive count and betting 3x your unit. Over time, however, your average roll will be zero and therefore your bets will be unchanged.
2) Of course this will have the undesired effect of amplifying standard deviation like a b*tch. Yes, you'll wind up with the same +/- over the very long haul but in the short term, it'll be a roller coaster.
Then there is the practical matter of how to perform a dice roll at the table. That's not too hard. During each round of play, remember the first card that hits the table between, say, 1-7 (count ace as a "1") and subtract 4 from that number. 1 would become -3, 7 would become +3. If no A-7 cards come into play on the round proceeding your bet, just use zero and leave your bet unchanged.
My thinking here is to break up the somewhat linear relationship between count and bets.
OK, I put on my asbestos jammies, flame away! :whip:
vQ
As I understand it, raising bets as the count goes up and lowering bets when the counts go down is a dead-giveaway for a CC/AP. If a TC of one or greater means a net advantage over the house, why not incorporate a random multiplier/divisor into the bet?
Normally, when it comes time to bet, you determine your RC, calculate your TC, subtract 1 and that gives you the bet unit multiplier. If your bet unit is $10 and your multiplier is 3, you'd be $30, etc, etc.
Just for visualization purpose, suppose you had a 7-sided with you but instead of 1-7 on the dice, you'd have -3 through +3 (-3, -2, -1, 0, 1, 2, 3). At any multiplier >=1, you'd roll the dice and adjust your bet accordingly.
This means that sometimes you'd start with unit multiplier of 4, roll the dice, get -2 and wind up placing a $20 bet. Other times you'd start with a unit multiplier of 2 and roll +3 and be betting $50.
How does this effect the game in total?
1) Your betting appears chaotic during the short-term (ie, the time during which you're being observed for AP). Sometimes you're at an advantage and betting flat, sometimes you're at barely a positive count and betting 3x your unit. Over time, however, your average roll will be zero and therefore your bets will be unchanged.
2) Of course this will have the undesired effect of amplifying standard deviation like a b*tch. Yes, you'll wind up with the same +/- over the very long haul but in the short term, it'll be a roller coaster.
Then there is the practical matter of how to perform a dice roll at the table. That's not too hard. During each round of play, remember the first card that hits the table between, say, 1-7 (count ace as a "1") and subtract 4 from that number. 1 would become -3, 7 would become +3. If no A-7 cards come into play on the round proceeding your bet, just use zero and leave your bet unchanged.
My thinking here is to break up the somewhat linear relationship between count and bets.
OK, I put on my asbestos jammies, flame away! :whip:
vQ