Lonesome Gambler
Well-Known Member
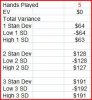
First of all, I'm 100% aware that I run the risk of losing all my money over the long run. That said, let's say I want to play some $25 CSM games (don't ask), and I plan on setting a limit of $100 on my potential wins. With a $300 BR, is it even worth considering that I could wind up with $100+ more times than not, and to a significant enough degree to make it worth a 40 minute trip to the casino twice a week? I don't have the ability to run any sort of sim, and I know that the math is foolish, but from playing many sessions at home with $25 flat bets, the results were typically something like this:
1: Win $150
2: Win $112.50
3. Win $112.50
4. Lose $300
5. Win $100
5. Lose $300
6. Win $100
7. Win $150
So, in this scenario (with each trip costing about $5 each in transportation), I would have made a total of $125, which ends up being about $13 a trip for a total gameplay of less than 30 minutes per trip. Not exactly lucrative, I know, but I want to know just how probably a scenario like this could be. Again, it's on a CSM, so we're just talking BS, flat bets.
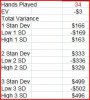
Now, I know that over the long run, I'm still looking at approximately a 1/2% house edge (CSM, S17, DAS, SA1, NS), but would it be in any way reasonable to think that, with a $300 BR, I could ride the flux to the $100 mark often enough to make a long-term (albeit humble) profit if I always stop as soon as I hit that mark?
1: Win $150
2: Win $112.50
3. Win $112.50
4. Lose $300
5. Win $100
5. Lose $300
6. Win $100
7. Win $150
So, in this scenario (with each trip costing about $5 each in transportation), I would have made a total of $125, which ends up being about $13 a trip for a total gameplay of less than 30 minutes per trip. Not exactly lucrative, I know, but I want to know just how probably a scenario like this could be. Again, it's on a CSM, so we're just talking BS, flat bets.
Now, I know that over the long run, I'm still looking at approximately a 1/2% house edge (CSM, S17, DAS, SA1, NS), but would it be in any way reasonable to think that, with a $300 BR, I could ride the flux to the $100 mark often enough to make a long-term (albeit humble) profit if I always stop as soon as I hit that mark?