Mathematical Proof that Progressions will never Overcome a Negative Expectation Game
- Thread starter iCountNTrack
- Start date
Both are untrue statements. If you graph the bankroll, it will be a wildly oscillating line, going positive and negative, with increasing amplitude over time. It does not asymptote to a continuous net loss, unless a table limit was imposed.psyduck said:
Given enough time, you're guaranteed to win, per QFIT, and it only takes once.
The probability of going broke is exactly zero. The probability of being ahead at some point is greater than zero. Therefore, given enough trials, you're going to win. Eventually.
...
The bias against progressions is understandable and justified (and I share it), but it's clouding many people's ability to think objectively about the question. Thorp was correct.
psyduck
Well-Known Member
Why do you keep talking about bankroll? Bankroll is not profit. Your unlimited bankroll is not your unlimited profit. Can you show me two things:johndoe said:
(1) the graph of profit (y) vs ever increasing number of plays (x).
(2) the equation from which the graph is created.
aslan
Well-Known Member
Infinity is a long time. You may never get to your first win. At any point in infinity, you still have an infinity to go. View attachment 7123 You are caught in an endless series of denial. :laugh:johndoe said:
Attachments
Each time a martingale is restarted after a 1 unit win could be the beginning of a disastrous sequence where losing continues until the end of time. Chance of a disastrous sequence never happening given all the time in the world approaches 0 just like the chance of never winning until the end of time approaches 0. So which is prevalent? We have this hint: In a negative EV game the expectation is to lose an amount approaching infinity for the committed martingale player.johndoe said:
21gunsalute
Well-Known Member
The probability that neither party will concede in this infinitely ridiculous debate approaches infinity.
You still do not understand. Unlimited bankroll means that you can keep playing until you have a single win. At that point, you have a profit.psyduck said:
As for the graph, I'll point you to qfit's own:
http://www.blackjackincolor.com/useless4.htm
It's disastrous for any finite bankroll of course. But there is a clear upward trend, is there not?
Go read your post again. You were the one who said the gun would always fire, given enough pulls. You've provided a nice analogy that exactly proves my point (and Thorp's). Are you admitting your analogy is incorrect? Will the gun ever fire, or not?QFIT said:
The only case that's being excluded is the one where no hand is ever won, for an infinite time. For this to be the case, the odds of winning would need to be identically zero. Because the odds of winning are nonzero, there is a guarantee of a win within an infinite time. You can call it "almost surely" if you like, but it's as close to certain as anything is.
Your attempt to lump me in with "progressionists" is nothing less than insulting. You know full well that I agree that progressions are completely worthless in any realistic situation. Once again, I'm arguing only that there is no proof here that Thorp's statement was debunked.
psyduck
Well-Known Member
In a negative expectation game, martingale works only in the sense that you quit playing for good after making a profit. If winning one unit is your sole goal, any other system can do it because of variance in the short term.johndoe said:
However, if you keep playing the negative expectation game, your cumulative profit = (your disadvantage)*(total wager). It will never become plus. The more you play the more you lose.
Your cumulative profit is proportional to your total wager, but the slope is negative. How can you make the equation (cumulative profit) = -0.5%*(total wager) positive?
21gunsalute
Well-Known Member
Ah, but you're assuming that it's a given that you will eventually have a single win. That should not be a given statement but an if-then statement. The condition is only true if you have a single win and one cannot assume that one will have a single win at any point in the future.johndoe said:
Other systems (or finite table limits) "can" do it if you're lucky. But over time, the bankroll function always decreases and asymptotes to a pure loss of slope -EV.psyduck said:
With martingale, like I said, the bankroll is a diverging, oscillating function that grows with magnitude over time. If you keep playing, you'll always go positive and negative at various times. Pick a positive time, which, per QFIT's example, will always arrive, and you're a winner.
Your equation describes the expectation at any specific number of hands (or total wager), but because the function is so unstable, it's a poor predictor.
What's the sum of the series 1-2+3-4...? But what are the values you'll actually see? It all depends on when you decide to stop.
The condition is true if the probability of a win is greater than zero; i.e. you have some chance of winning a round. That's a condition of the problem.21gunsalute said:
You can't guarantee a win at any specific time, but you can guarantee an eventual win, just like QFIT said in his russian roulette analogy.
21gunsalute
Well-Known Member
No, probability and actuality are not the same.johndoe said:
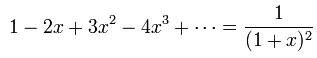
Your cumulative profit is only whatever you made at the point you decide to stop. Since you get to choose to stop where you want, you can claim whatever profit you wish.psyduck said:
Can you prove to me it's always negative? Or never positive? Look at the series example I just gave and think about it carefully.
You can't make it positive for all or any arbitrary future point; you have to end on a point where there is a profit. Because the series oscillates, this point will occur ('almost certainly'!). This does not happen when there is a table limit, because eventually the oscillation can't grow large enough to maintain any positive points. THEN the series asymptotes to -0.5*(wager).
iCountNTrack
Well-Known Member
nth Attempt
Correct. But will we ever see the value of 1/4 occur?QFIT said:According to Euler and later shown by Niels Abel, the sum of 1-2+3-4 taken to infinity is 1/4. The general case is:
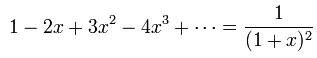
In your example, x=1 and the sum is 1/4.
No, you get an oscillation from positive to negative values that grows in amplitude indefinitely. Just like in a martingale. That's why stating it purely in terms of EV is a poor reflection of what's going on mathematically.